Clausura topológica

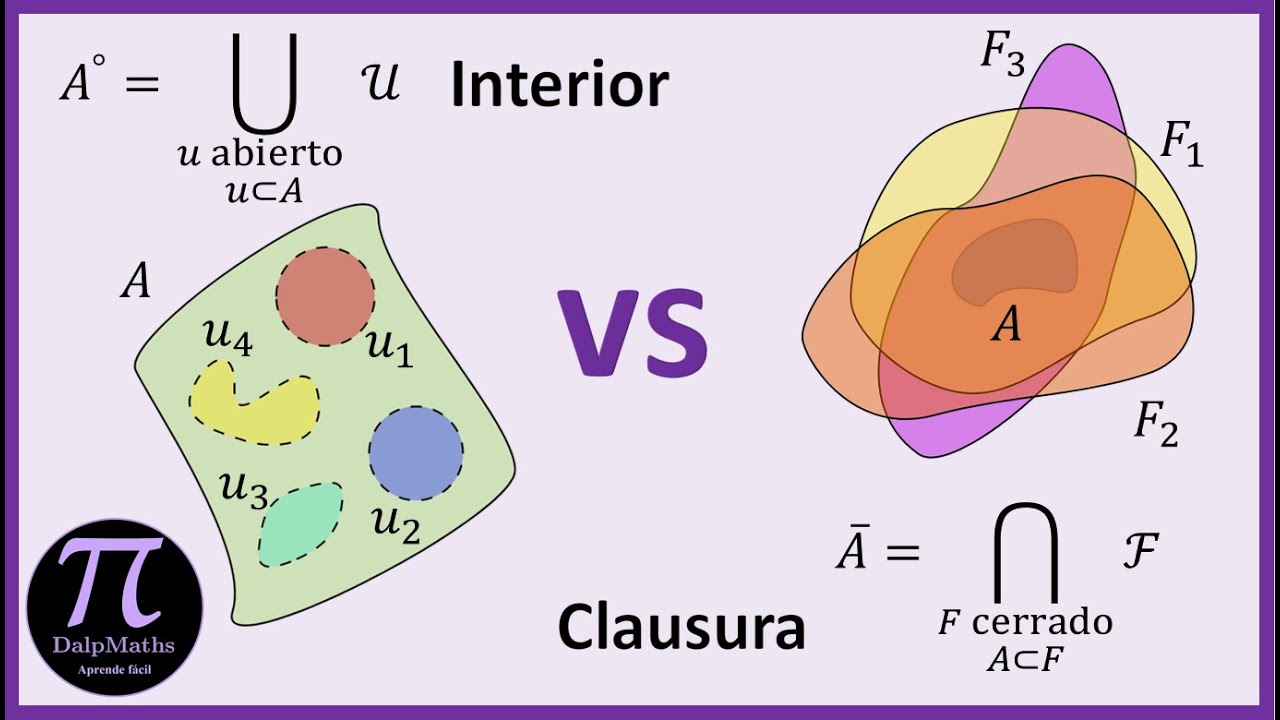
En un espacio topológico ${\displaystyle (X,T)}$ la clausura, adherencia, cerradura o cierre de un subconjunto E es el conjunto:

${\displaystyle {\bar {E}}=\{x\in X|\forall N(x):N(x)\cap E\neq \emptyset \}}$

donde ${\displaystyle N(x)}$ es el símbolo para un entorno de x. Es decir, es el conjunto de todos los puntos de adherencia de E.

Una manera de definir un conjunto cerrado es diciendo que "un conjunto es cerrado si y sólo si es igual a su clausura".

Equivalentemente la clausura se puede definir mediante

${\displaystyle {\bar {E}}=E\cup E'}$

donde ${\displaystyle E'\ }$ es el conjunto de los puntos de acumulación de ${\displaystyle E\ }$.

La clausura de ${\displaystyle E\ }$ es también la intersección de todos los conjuntos cerrados que contienen a ${\displaystyle E\ }$.

Propiedades

Sea (X, T) un espacio topológico entonces:

• ∅^c = ∅
• M ⊂ M^c para todo M elemento del conjunto potencia de X.
• (M ∪ N)^c = M^c ∪ N^c
• ${\displaystyle M\subset N\ \rightarrow M^{c}\subset N^{c}\ }$
• La clausura de la intersección de dos conjuntos está contenida en la intersección de sus respectivas clausuras: (M∩N)^c ⊂ M^c ∩ N^c.^[1]​ Sin embargo, la contención recíproca no siempre se cumple.
• (M^c)^c = M^c para cualquier miembro del conjunto 2^X
• La adherencia ${\displaystyle M^{c}}$ es un conjunto cerrado.
• La adherencia ${\displaystyle M^{c}}$ es el menor conjunto cerrado que contiene al conjunto ${\displaystyle M}$.^[2]​

Referencias

Bibliografía

• Baker, Crump W. (1991), Introduction to Topology, Wm. C. Brown Publisher, ISBN 0-697-05972-3 .
• Croom, Fred H. (1989), Principles of Topology, Saunders College Publishing, ISBN 0-03-012813-7 .
• Gemignani, Michael C. (1990) [1967], Elementary Topology (2nd edición), Dover, ISBN 0-486-66522-4 .
• Hocking, John G.; Young, Gail S. (1988) [1961], Topology, Dover, ISBN 0-486-65676-4 .
• Kuratowski, K. (1966), Topology I, Academic Press .
• Pervin, William J. (1965), Foundations of General Topology, Academic Press .
• Schubert, Horst (1968), Topology, Allyn and Bacon .

Véase también

• Punto adherente